什么是摩尔定律

图1于1965 年4月19日由 Gordon Moore 在他的论文“Cramming more components to integrated circuits”（计算机历史博物馆）中发表。

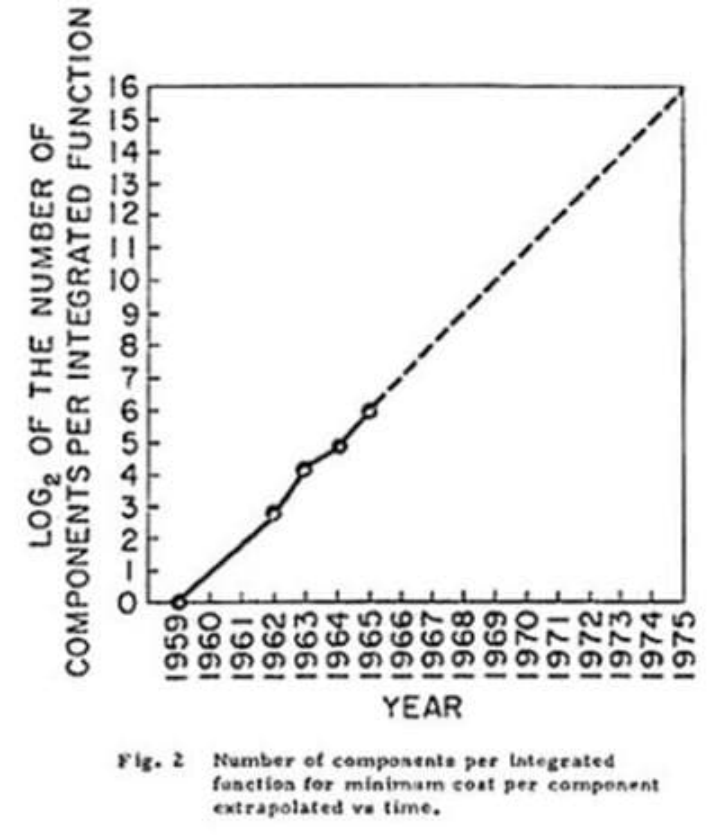
图 1 由 Gordon Moore 先生首次发表的“摩尔定律” 资料

该图的纵轴是每个集成功能（半导体芯片）的组件（晶体管）数量。此外，由于它被写成Log2，这表明晶体管的数量将呈指数增长。

不过，这个数字只写了1959年到1975年，不能读成“集成水平在两年内翻倍”。

之后，1968年与罗伯特·诺伊斯一起创立英特尔的戈登·摩尔在1975年修正了摩尔定律，称“晶体管集成度每两年翻一番”。截至目前，晶体管的集成度以“每两年翻一番”的速度增长。换句话说，半个多世纪以来，摩尔先生 1965 年的预测一直是半导体行业的指南针。

而摩尔定律的延续背后还有另外一条定律。

登纳德缩放比例定律

1974年，也就是摩尔先生修正摩尔定律的前一年，IBM（美国）的登纳德写了一篇论文，指出“按照一定的规律小型化会提高晶体管的速度，降低功耗，提高集成度”。宣布（图 2）。这被称为登纳德的“比例定律”。

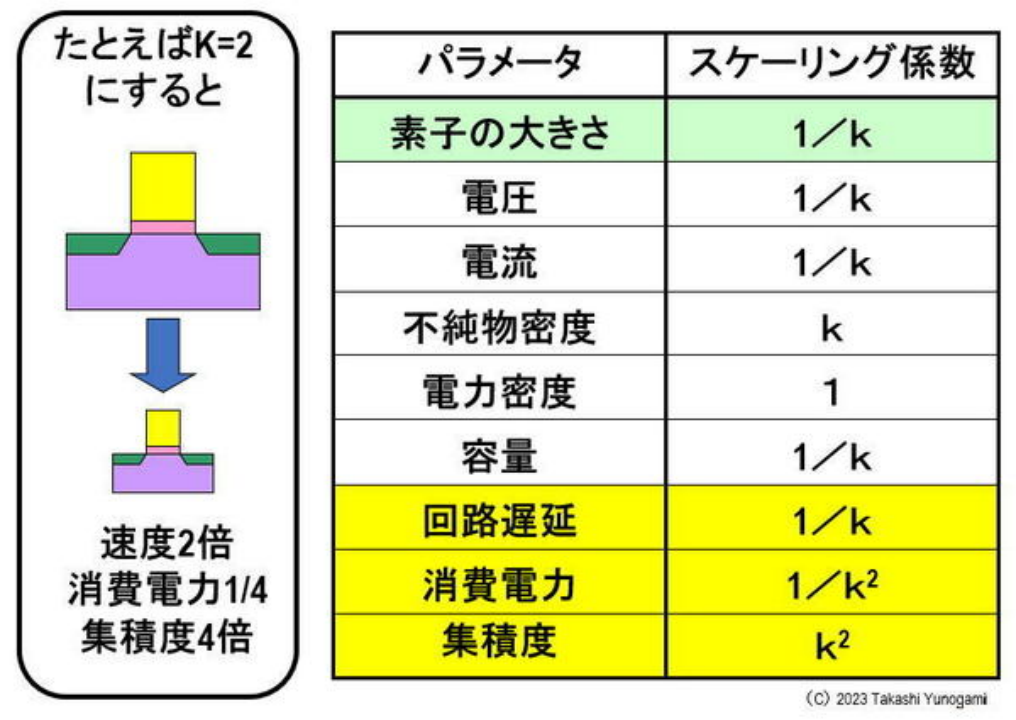
图2 Dennard 的比例定律 来源：“具有非常小物理尺寸的离子注入MOSFET的设计”，IEEE Journal of Solid-State Circuits SC-9 （5）

例如，如果我们将图3中的K=2代入，那么晶体管的电路延迟将减半（换言之，速度将增加一倍），功耗将是1/4，集成度将是4倍。此外，每个晶体管的成本也降低了四分之一。

换句话说，如果按照登纳德的“比例定律”将晶体管小型化，提速、功耗、高集成度、成本降低都可以一下子实现，不需要任何电路上的巧思。

简而言之，摩尔定律是增加晶体管数量的罗盘，登纳德的“比例定律”是小型化时性能更高的定律，是汽车的两个轮子，随之而来的是“晶体管集成度在两年内翻了一番，晶体管尺寸在同样的两年内缩小了70%”，这已经持续了半个多世纪（图 3）。

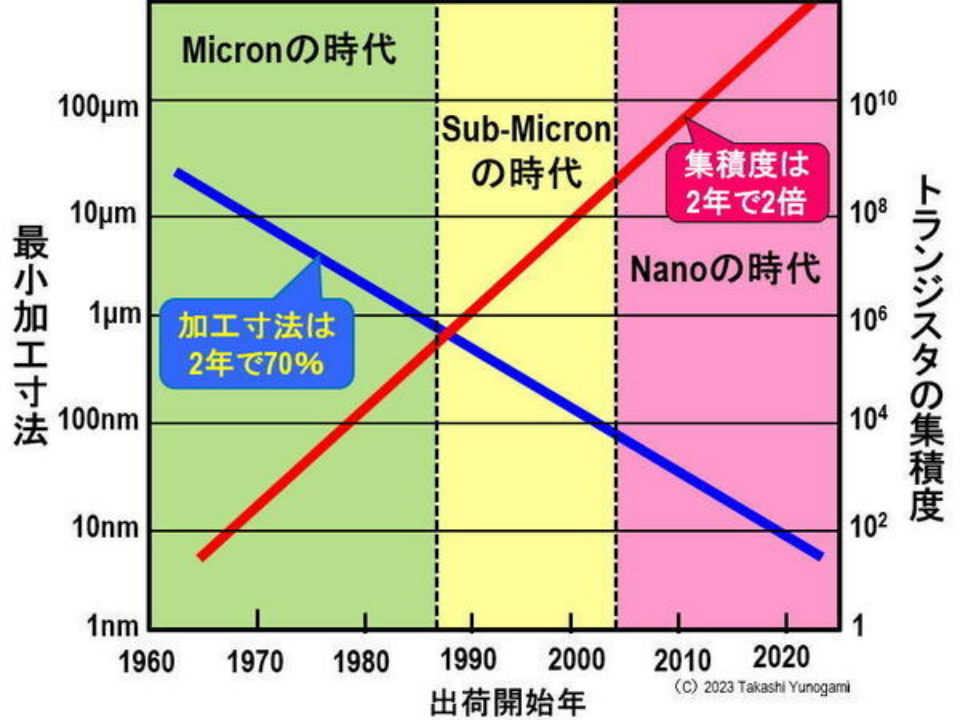
图3 延续50多年的摩尔定律（背后有登纳德比例定律）

摩尔定律的本质是什么？

让我们重温一下摩尔定律的本质。2023年2月20日，笔者参加了日本晶体管研究的领军人物、东京大学高木真一教授举办的“半导体器件入门”（科学技术主办）研讨会。想重新学习一下晶体管的基础知识，研究一下晶体管的技术动态。

听了高木教授的讲座，让我明白了摩尔定律本质的新含义。这是因为高木教授对摩尔定律的本质进行了如下解释（图4）。

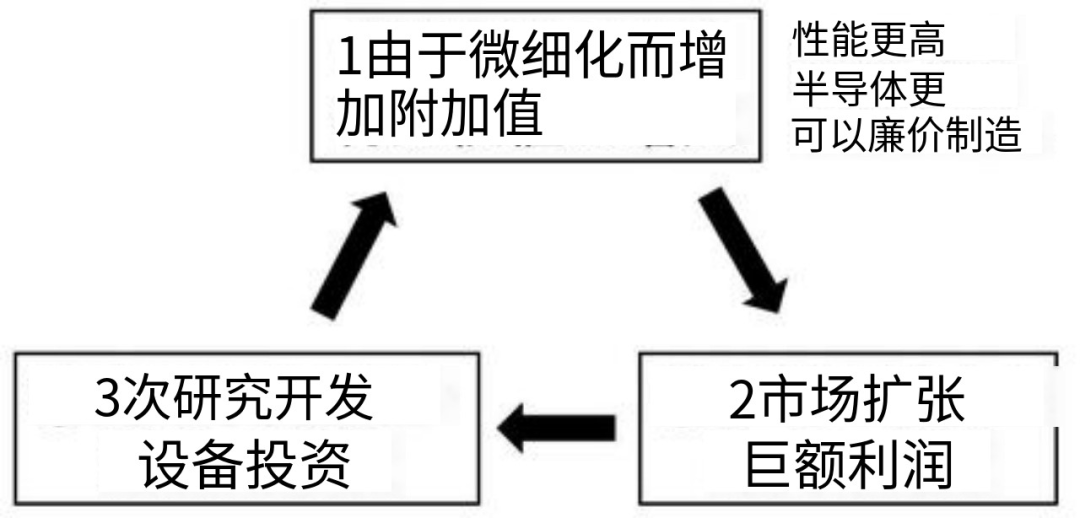
图 4 摩尔定律的本质

第一，晶体管的小型化提高了半导体的附加值。这是因为小型化使得以更低的成本实现更高性能的半导体成为可能。

第二，这种小型化和高集成度的半导体可以扩大市场并获得巨大的利润。

第三， 利润将用于下一步的小型化研发和资金投入。

也就是说，摩尔定律的本质就是让这个循环一直循环下去。而通过不断循环这个循环，摩尔定律一直延续了50多年。

下面，我们表明半导体制造商的成功取决于他们保持上述循环运转的能力。

Rapidus和台积电之间的巨大差异

笔者一直对日本新公司Rapidus持负面看法，Rapidus在2022年10月宣布2027年前量产2nm逻辑半导体，做不到的根本。

如果思考一下Rapidus是否能实现图4中的循环，就很容易理解为什么认为 Rapidus 不起作用。Rapidus已宣布到2027年将投资2万亿日元用于开发，3万亿日元用于量产，总计5万亿日元。这笔资金可能会暂时由政府补贴支付。

这对应于图 4 中的第三点，但不可能在第一点之后进行到第二点。换句话说，即使制造出2nm的逻辑半导体（虽然笔者认为很困难），也不可能用该技术实现“第三点，市场扩张和巨大利润”。这是因为没有无晶圆厂公司将生产外包给 Lapidus。如此一来，就无法获得“巨额利润”，也无法投入到2nm之后的下一个1.4nm。

另一方面，走在微型化前沿的台积电，成功循环了摩尔定律的循环。

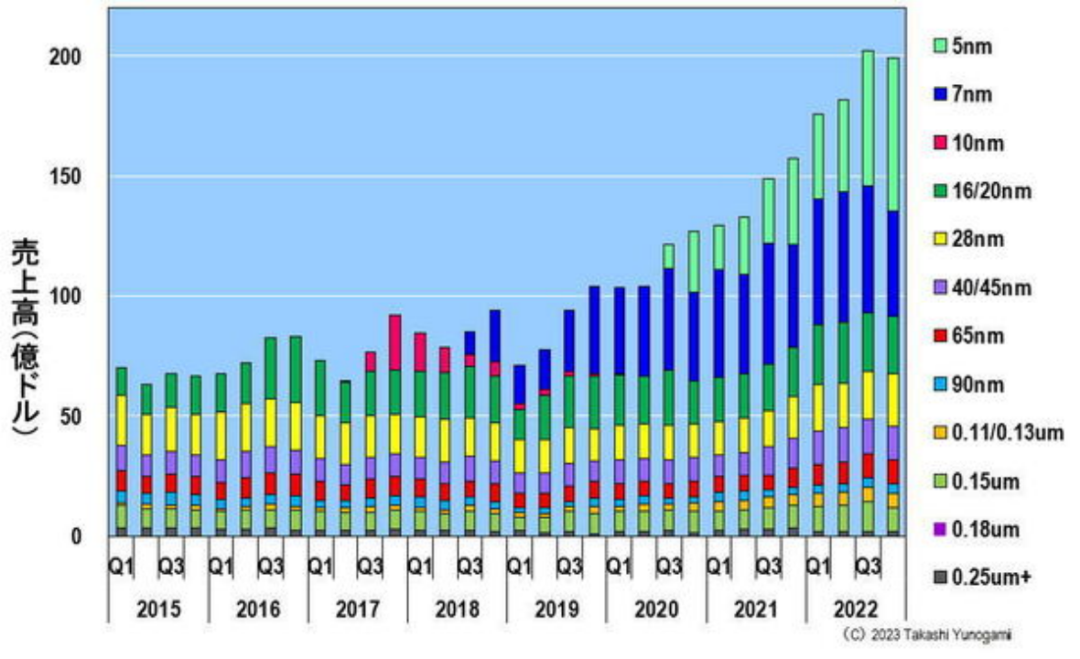
作为这一点的证据，如图 5 所示，他们已经成功地量产了最先进的半导体，并增加了销售额。尤其是在7nm之后，它成为了唯一的赢家，几乎垄断了最先进的半导体。因此，7nm及以下的销售额比以前更高。