84次浏览 发布时间：2022-12-13 07:15:40
三角形的证明题
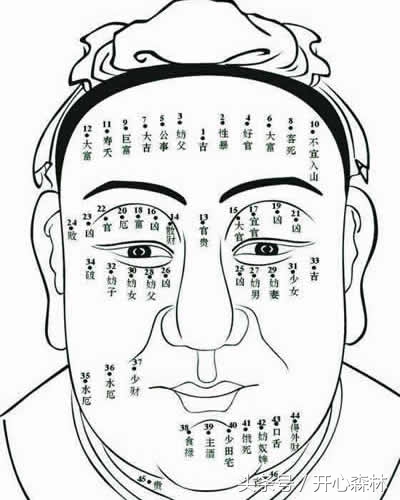
三角形ABC是直角三角形，D、E两点将斜边三等分点，∠DCE=α,
证明 tanα=3ab/(2c2)
证法1：如图α=90°-β-γ
tanβ=(a/3)/(2b/3)=a/(2b)
tanγ=(b/3)/(2a/3)=b/(2a)
tanα=tan(90°-β-γ)
=cot(β+γ)
这里要用到一个三角函数公式：
所以tanα=tan(90°-β-γ)
=cot(β+γ)
=（1-tanβtanγ）/(tanβ+tanγ)
=［1-(b/2a)(a/2b) ］/(b/2a+a/2b)
=(3/4)x2(
由于三角形ADG相似于三角形BDC，三角形BEH相似于三角形AEC，所以很容易得知，
G是AF的中点， H是BF的中点。因此有下列表达：
tan∠ACG=a/2b
tan∠BCH=b/2a.
由于tanα=cot(90∘−α),可以得出：
上面最后一步用到了勾股定理。
证法3：如图做两条底边的垂线，
tanβ=(b/3)/(2a/3)=b/2a
tan(α+β)=(2b/3)/(a/3)=2b/a
tanα=tan［(α+β)- β］
=［(tan(α+β)-tanβ) ］/ ［1+tan(α+β)tanβ］
=(2b/a-b/2a)/(1+2b/a. b/2a)
=(3b/2a)/(1+
/
)
=3ab/
